Prime factorization calculator

What is prime factorization?

What is prime factorization or what are prime factors? Prime factorization is a way of expressing a number as a product of prime factors. Any integer n can be expressed as a product of prime factors as follows n =p_0 ... p_n, where p_i > 1 and prime. While dealing with prime factorization, it is essential to have an understanding of prime numbers. A prime number is defined as an integer p such that p has 1 and p as its only factors/ divisors. Another closely associated term is coprime. Two numbers n_1 and n_2 are said to be coprime or relatively prime if and only if 1 is the only common factor between them. Note that for any two coprime numbers, neither one of them needs to be a prime number. Factorization and prime factorization are not equivalent, though related. To distinguish between the two terms, we can use an example. Let us factorize 30 30 = 5\times6 30 =3\times10 30 = 2\times3\times5

All the above are ways in which we can factorize 30. However, only the last statement is a prime factorization of 30. This is because all the factors in the last statement are all prime numbers i.e. their only divisors is one and themselves. You can try out other numbers using our prime decomposition calculator with step by step solution.

Theorem: For any number n, there exists only one prime factorization. However, the number can be factored/ decomposed in more than one ways.

How the prime factoring calculator with exponents works

Step 1 Enter a number on the text space provided and hit factorize ! button

Our Prime factorization calculator works by finding a list of all prime factors for a given number. The calculator then displays the results in various formats such as factor tree, exponent format etc. In addition, the calculator has an option to display all the factors of a given number. This allows user to compare and understand the real meaning of prime factorization. Unlike other online prime factorization calculator, ours gives you an opportunity to learn and understand prime factorization from different perspectives. In particular, the calculator shows you the relation between the divisors and prime factors of a number.

Factor Calc solution Step 1

With appropriate display of factors and divisors, users can easily pick out other important elements between numbers such as GCF/ GCD and LCM.

The calculator works well with both large and small numbers. It can be used for any number less than 1,000,000,000.

Prime Factor Calc solution Step 2

How to find the prime factors of a number

There are two basic methods that we use to find the prime factors of any number namely trial and error division and factor tree method.

Factorization by trial division

This method is quite easy to follow and is useful in finding the prime factors for smaller numbers. First we start off by dividing the number with the first well known prime factor 2 . If 2 divides n (i.e. it divides n without a remainder), then 2 is a factor of n. If 2 fail, then we try the next prime number 3 and so on for all prime numbers less than n. Next we take the quotient and repeat trial division with prime numbers less than n until we find a factor. The process is repeated until the remainder is less than 2 in the last iteration. Once we have hit the last iteration, we collect all the resulting factors and compare their product with our initial number n. If the two are equal, then we have achieved prime factorization.

Example:

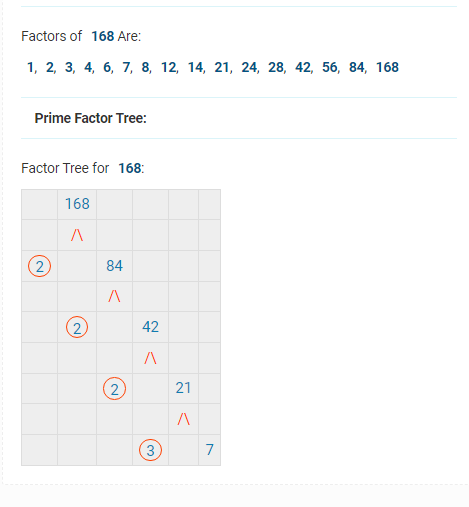
Find the prime factors of 168

168 \divide 2=84 save 2

84 \divide 2=42 save 2

42 \divide 2=21 save 2

21 \divide 3=7 save 3,7

168 = 2 \times 2 \times 2 \times 3 \times 7

168=2^3 \times 3 \times 7

More Examples by the prime factor calc

Prime factorization by factor tree

A factor tree allows one to visualize the factorization process by displaying the relation between a number and its factors. From the factor tree, it is easy to pick out the prime factors for a particular number.

Example 3: Factor 240 using a factor tree

Application of prime factorization

Our prime factorization finder is fun and easy to use. In addition it gives you ton of useful information that you can apply in other areas of mathematics. Prime factors are quite useful in mathematics and can be applied in various calculations.

Finding GCD/ GCF and LCM using prime factorization

When factoring polynomials it is essential to find the prime factors of its coefficient in order to get its prime factorization. Prime factors are also used in finding the GCD and LCM of numbers. For example when finding the GCD of a given numbers, we find prime factors of each then pick the factor with the lowest power that is common between the numbers. The GCD is then found by finding the product of these factors.

Example: Find the GCD of 168 and 72

Factorize (168) = 2 \times 2 \times 2 \times 3 \times 7=2^3 \times 3^1 \times 7^1

Factorize (96) = 2 \times 2 \times 2 \times 2 \times 2 \times 3 = 2^5 \times 3^1

Thus, GCD(168,96) =2^3 \times 3=24

To Learn more about GCD, visit GCF Calculator

On the other hand, when finding the LCM, we take the highest power of the common factors and find the product.

E.g. LCM(168,96) = 2^5 \times 3^1 \times 7^1 = 672

To Learn more about LCM, visit LCM Calculator

Practice factorization with solved examples