Completing the square Solver A Calculator With Step by step Solution/Explanation

Solving quadratic equations by completing square method Calculator

Quadratic equations are mathematical expressions of the form ax^2+bx+c=0 where a=/0.

Different solution strategies can be used to find a solution or solutions to the above or similar problem. A solution or a root to a quadratic equation is basically a number that satisfies the equation. Thus, if we substitute the number on the left hand side of the equation we will get a value equivalent to the value on the right hand side of the same equation.

There are 3 classical methods of finding solutions/ roots to any quadratic equation namely

• Factoring method
• Completing square method
• Quadratic formula method

The quadratic formula completing the square calculatorat is a free online tool that helps you solve quadratic equations using the completing square method

The factoring method is one of the basic strategies of finding solutions to a quadratic equation. Nevertheless, this method is only applicable to a specific class of quadratic equations. On the other hand, nearly all types of quadratic equations can be solved using the quadratic formula and complete the square methods.

The factoring method is one of the fundamental solution strategies for solving quadratic equations. Considering that not all such equations can be factored, the completing square method comes in handy.

In the completing square method, we manipulate the given equation by adding or subtracting the given terms until we achieve a perfect square on the left hand side of the equation. With a perfect square on the Left hand side of the equation, we can then apply the square root property to find a solution.

In general the calculator tries to complete the square to form a true equation for a given equation

Solve by completing the square calculator : A free online tool

Our complete the square calculator is a free online tool that helps you solve quadratic equations using the completing the square method. This calculator not only gives you the solution or roots to your given quadratic equation, but it will also show you a step by step solution to the equation. In fact, the calculator solves equation with either real or complex roots.

Solving a quadratic equation by completing the square method Solver with step by step answer

To illustrate how you can go about solving a quadratic equation using the quadratic equation by completing the square solver, we will apply an example. The method applied here is the systemic way of handling the same problem.

Example 1

Given the quadratic equation: ax^2+4x+1=0

The steps below illustrate a step by step solution strategy to solving a quadratic equation using the completing the square method.

Step 1:

If a\ne 1, divide the equation through by a to have a unity coefficient as the leading coefficient

The result will be

x^2+\frac{4}{a} x+\frac{1}{a}=0

Next add the constant term (\frac{1}{a}) to the right side of the equation and subtract the same from the left hand side of the equation.

x^2+\frac{4}{a} x=-\frac{1}{a}, to make the above illustration more workable, let’s substitute \frac{4}{a} with b, and c with 1/a thus we can re-write the above equation as follows.

x^2+bx=c

We add ½ of b squared on both side of the equation

Thus we have x^2+bx+\frac{b^2}{4}=c+\frac{b^2}{4}

The left hand side of the equation is now a perfect square and can be written as follows

(x+\frac{b^2}{2})^2=d, where d is a constant term representing c+b^2/4

Finding the square root on both side of the equation we obtain x+\frac{b^2}{2}= \pm\sqrt{d}

Example 2:

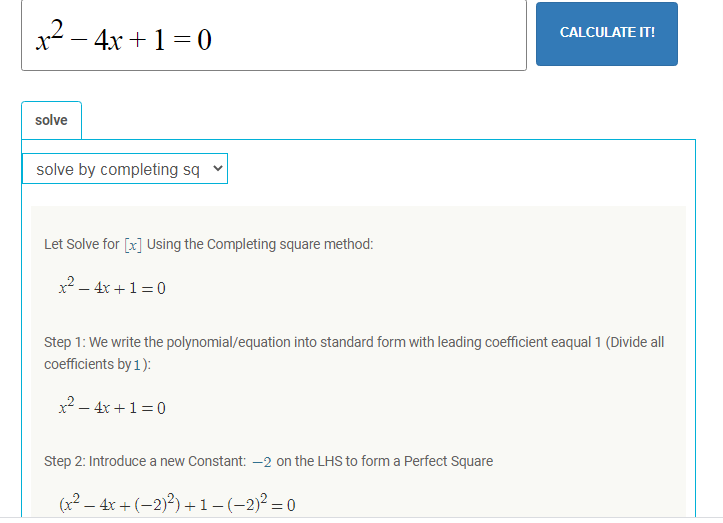
• x^2-4x+1=0
• x^2-4x=-1 (adding -1 on both sides of the equation)
• x^2-4x+4=-1+4 ( Adding square of -2 on both sides of the equation)
• x^2-4x+4=3
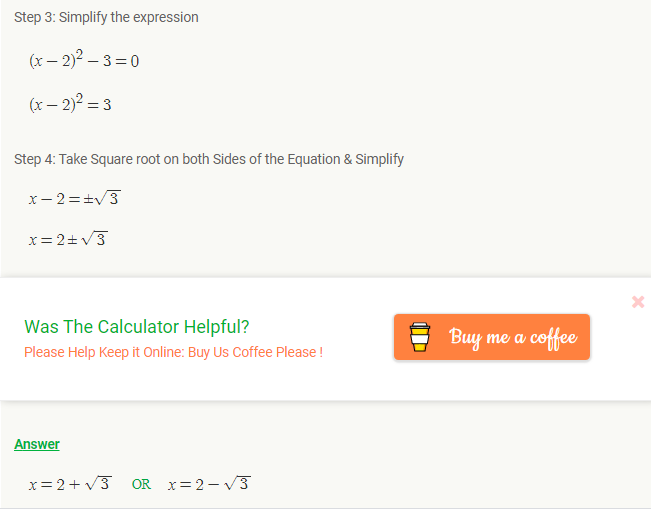
• (x-2)^2=3
• x-2=\pm\sqrt{3}
• x=\sqrt{3}+2, or x=-\sqrt{3}+2 are the two solution to the quadratic equation above.

Certainly, solving the above problems manually can be time consuming. Moreover, you are most likely to hit an error while working out the problem. With our quadratic equation calculator, you can solve any type of quadratic equation using the completing the square method. Better still; the calculator gives you a step by step solution with all the workings.

Solve by completing the square calculator worked examples

The example below illustrates how the completing square method free online calculator works. It is easy to see that the calculator gives you a step by step solution including all the workings. The solutions are generated automatically in real time. Our online quadratic equation calculator is reliable and free.

Solving quadratic equations by completing the square calculator

Below is a step by step illustration on how to solve quadratic equations using the completing square calculator. Solving quadratic equation by completing square calculator is easy and straightforward. You can solve just any equation of degree 2 just by entering the given equation in the text area given then hit the calculate button

Solving quadratic equations by completing the square calculator : Step by step procedure

How to solve a quadratic equation using the complete the square free online tool

To solve any quadratic equation using the complete the square method, follow the following steps.

1. Type in your equation in the text area provided, See below for a list of acceptable characters
2. Once you have entered your equation correctly, hit the Enter Key from your keyboard or click on the calculate Button
3. The online tool for quadratic equations will generate a solution to your math problem
4. Next, step is to use the generated solution as required

Free Quadratic equation solution generator

Our free quadratic equation solver helps you generate solution to any quadratic equations online. The tool is a free online calculator for solving quadratic equations using the completing the square method.

Completing square formula calculator

The formula for solving a quadratic equation using the completing the square method relies on the square root principle. Given any quadratic equation of the form ax2 + bx + c = 0 for x, where a ≠ 0, we can apply the completing the square method to find a solution.

Our complete the square calculator saves you the hard work by giving you an appropriate and accurate solution to solving quadratic equations using the complete the square method.

The free online quadratic equation solution generator helps you generate solutions to quadratic equations fast and with accuracy.

Completing the square calculator with steps

Our completing square calculator shows step by step solution with all the workings.

The calculator is a perfect solution/ roots generator for quadratic equations. Further, the calculator shows all the workings in a step by step method. The calculator generate solutions using the square root property

what's a perfect square

A perfect square is a number that can be expressed as a product of two numbers. Similary we can factorise an equation into its resulting products or factors. The complete square method, solves quadratic equations by creating a perfect square

Learn how to solve quadratic equations using the completing square method

Perhaps it is best if you learnt math through examples. Checkout our algebra examples, each with a step by step solution. The Examples will also guide you on how to use this equation calculator to solve your algebra problems.

Go to Solved Algebra examples with Steps

Acceptable Math symbols and their usage
If you choose to write your mathematical statements, here is a list of acceptable math symbols and operators.

• + Used for Addition
• -Used for Subtraction
• *multiplication operator symbol
• /Division operator
• ^Used for exponent or to Raise to Power
• sqrtSquare root operator

What’s more or what are the limitations of the online algebra calculator

We love to hear your feedback. If you encounter any problems while using this calculator, please let us know: Want to see more features? Send us your recommendations and app ideas. We are always working hard to make algebra easy and fun.