Factoring calculator with steps: Factor Expressions

In general, the first step in factoring any algebraic expression is to determine whether the terms have a common factor. Factoring or factorisisng is the process of spliting an expression into simpler expressions whose product equal to the original expression.

Our factoring polynomial calculator can factor any algebraic expressions into a product of simpler factors/ prime factors. The calculator works for any binomials, trinomials, monomials, rational and irrationals. The calculator shows you all the steps by utilizing various techniques such as grouping, quadratic roots formula, difference of 2 squares factoring etc.

For Binomials, quadratic, polynomial expressions or number into its prime factors. Enter math expression to find its factors

What we can factor? All the following can be factored using our online factoring solver with steps

• Numbers i.e. rational or irational, e.g. 15,20,25
• Polynomial => 2x^2-3x+3   (A polynomial is an algebraic expression comprised of variables, constants and exponents combied by adition, multiplication, substructions, no division by varriables).
• Binomial=> algebraic expression which contains only two terms with adition or substruction 2x-5: two terms polynomial

• Trinomial => 3 term polynomial
• Quadratic => Second degree, single varriable polynomial
• Rational => Numbers that can be expressed in the form p/q, where p,q are intergers and 2x^2-3x+3q \neq 0

Factoring expression Calculator for Binomials, quadratic, polynomial expressions

This calculator will help you factor any algebraic expressions into its factors. The calculator works on any algebraic expression.

Factor Expression free online calculator

To learn how the factor calculator works, click on the “Try It” button to view the solutions with steps. You can also enter an expression on the input field provided above and click the “factor” button to view the solution.

Try typing these expressions into the calculator, click the blue arrow, and select "Factor" to see a demonstration. Alternatively, you can use the examples provided as a template to create and solve your own problems.

Problem: 4x^2-9

Solution:  (2x+3)(2x-3)

How the free factorizing calculator works

Factorization is the process of breaking a complex expression into simpler terms. To factor an expression completely, one needs to re-write the expression as a product of its irreducible products. Thus, an expression is factorable if and only if it can be written as a product of two or more factors under multiplication.

For example 2x-2= 2(x-1) , in this example, 2 and x-1 are the factors of 2x-2, the factors are prime / irreducible since the cannot be Brocken further into simpler factors with rational

More examples

Example: x^2+2x-8

Solution: (x-2)(x+4)

Example: x^21

Solution: (x-1)(x+1)

Example: 2x^2+2xy-8x

Solution: 2x(x+y-4)

Example: (x-3)(x^2-1)

Solution: (x-3)(x+1)(x-1)

From the examples above, it is evident that an expression is said to be fully factored, if it can be fully expressed as a product of simple factors. In addition, an expression can be made of any combination of terms and factors.

Factor a Number into its prime factors calculator

Our factorization calculator helps you re-write any number as a product of its prime factors. Any number can be written down as a product of its prime factors through factorization process. The process involves division iteration with the smallest divisor of a given number.

Factorize a rational number into prime factors

Any rational number can be factorized into a product of prime factors. Given a rational number q, we can write it as a product of its prime factors e.i q= p0 \times p_1 \times p_2….. \times pn, where p_0,p_1,p_2…. p_n is a finite set of prime factors or divisors of q. Our factor calculator can help you factor any number to its prime factors. To factor a number, simply enter the number in the given text area, click on the factor button to proceed.

How the online factor calculator works

There are several techniques that are applied when factoring an expression. The technique applied depends on the given expression. However, factoring an expression is not always obvious and not all expressions can be factored. Learning how to factor an expression is a useful technique that is useful in solving or finding the roots of polynomials.

Factor an expression by grouping calculator

This is one of the fundamental techniques applied in factoring expressions. The method groups terms within an expression by finding the common factors. 

Example 1: 2y(x+3)+5(x+3) 

Solution: since (x+3) is a common factor between the terms, the expression can be rewritten as 2y(x + 3) + 5(x + 3)  = (x+3)(2y+5)

Example 2: factor 2xy-2y^2-2x+y

2(x-y)(y-1)= 2xy-2y^2-2x+y

Example 3: factor ax - ay - 2x + 2y

Solution: a(x-y)-2(x-y)=(a-2)(x-y)

Notice that (a-2) and (x-y) are the factors of ax-ay-2x+2y

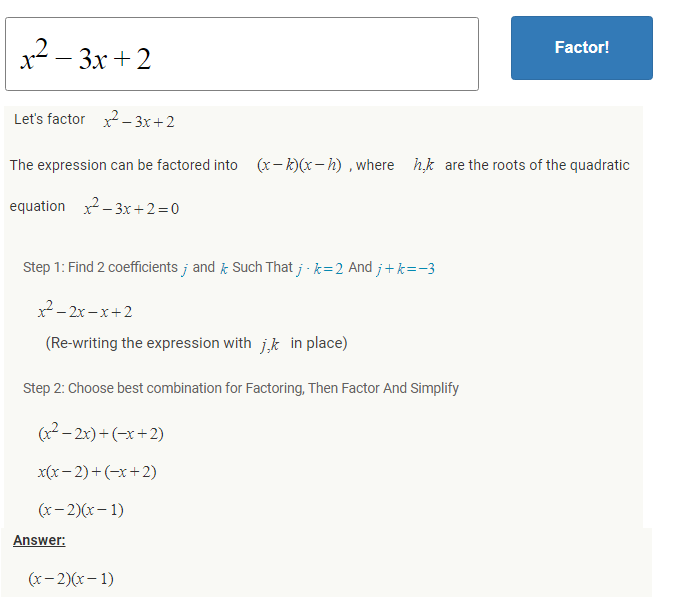
Factoring trinomial expression

A trinomial is an algebraic expression composed of 3 terms which are combined with addition and subtraction. Usually, a trinomial is a product of two binomials. Most factoring problems involve trinomials and can be solved using several methods.

Examples of trinomials expressions and how to factor them 

1. 2x^2-2x+1
2. x^2+3x-4

The most commonly used method to factor a polynomial ax^2+bx+c with a,b,c \neq 0 is by finding to constants h,k such that h+k=b and h \times k=c \times a. the constants h,k are also the roots of the equation ax^2+bx+c=0

Example: x^2-2x+3

Solution: Using trial and error method, you can find 2 constants 3 and -1. We can then re-write the expression as follows

x^2-x+3 = x^2-1 \cdot x+3 \cdot x+3

note that  -1+3=2 and -1 \cdot 3=3 \cdot 1

we can now group the expression using parenthesis as follows

x^2-1 \cdot x+3 \cdot x+3=(x^2-x)+(3x+3) =x(x-1)+3(x+1)  [factoring out the like terms]

  =(x+3)(x+1) factoring further

 We now have (x+3)(x+1) as the factors of  x^2-2x+3 

Factoring binomial expression by difference of 2 squares method

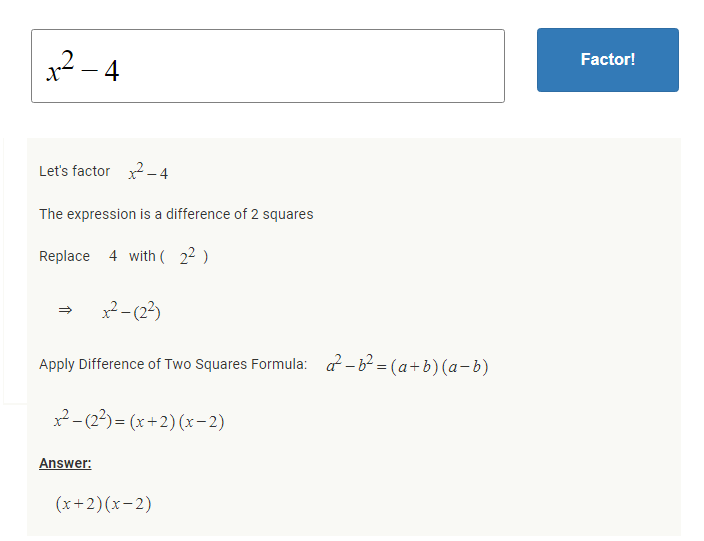
A binomial is an algebraic expression that is comprised of two terms. A binomial expression can be factored using various methods. Difference of two squares is the most common strategy that is used to factor a binomial expression.

This method will only work if and only if the binomial is made up of two perfect squares separated by a subtraction sign e.g.  x^2-4

The general formular for the difference of 2 squares factoring method is

  a^2-b^2 = (a+b)(a-b),

Example:  x^2-4 = (x+2)(x-2), notice that x^2 and 4 are perfect squares whose square roots are x and 2 respectively.

Factorize a rational expression into its constituent prime factors

When factoring an expression, the aim is to reach a prime factorization. By reaching the prime factors means that the expression cannot be factored further.

For example given the expression x^3+x^2-x-2

The expression can be factored as follows,

x^3+x^2-x-2 = (x^2-1)(x+2)

We notice that x^2-1 is a difference of 2 perfect squares and that is not a prime factor since it can be factored further into (x+1)(x-1), thus x^3+x^2-x-2 =(x+1)(x-1)(x+2) is the complete factorization of the expression.

Factor polynomial calculator

A polynomial is an algebraic expression involving variables, exponents and coefficients with addition and subtraction as the only operations between the terms. While some polynomials can be factored into irreducible/ prime factors, others cannot be factored.

For polynomials of degree greater than 2, there is no general factoring procedure for such. A trial and error method is applied in such a case. Our factoring polynomial calculator gives you instant solution or factors for any polynomial that is factorable. This helps you avoid the long procedure of trial and error which may not be a great approach.

To factor a polynomial using our factorization calculator, simply enter an algebra expression on the input field provided, hit the factor button to calculate.

Create equivalent expressions by factoring calculator

Factoring an expression, means creating an equivalent expression or factors of the original expression such that when multiplied/simplified they result into the initial expression. Creating equivalent expression or factoring can be a tedious expression especially when dealing with polynomials of a higher degree.

Our factoring calculator lets; you find factors for a given algebraic expression instantly.

Factor the trinomial completely calculator

A polynomial is said to be completely factored if it is written as a product of prime factors. When factoring a polynomial, the resulting factors are not always irreducible and my need further factoring. Our factoring calculator for polynomial lets’ you factor an expression completely resulting in a prime factorization. The calculator rewrites the expression by factoring out calculator.

Factor quadratics special cases calculator

When factoring an expression, some special cases arises which can be factored using some special formula.

Difference of 2 square formula is an example of a special factoring case. Given an expression of the form a^2-b^2 , where a^2 and b^2  are perfect squares separated by a minus sign, the expression can be factored using the negative square difference formula i.e. a^2-b^2=(a+b)(a-b). This formula can be extended to all algebraic expression of this form.

Factoring by grouping solver with steps

Factoring an expression by grouping is one of the fundamental factoring techniques. This method groups terms within an expression depending on the similarity. For example the expression

2x+2y-xy-x^2 can be grouped as follows (2x-x^2)+(2y-xy). From the grouping, it is easy to factor the like terms out as follows (2x-x^2 )+(2y-xy)=x(2-x)+y(2-x) , the expression can be factored further into

(2x-x^2 )+( 2y-xy)=x (2-x) +y(2-x)=(2-x)(x+y)