Conics Section calculator is a web calculator that helps you to identify conic sections by their equations
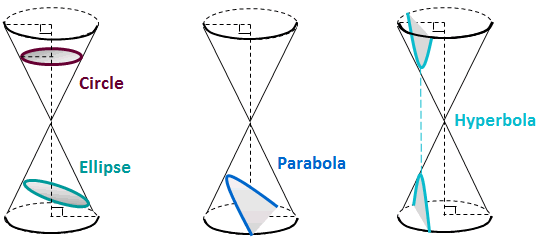
Conics are a set of curves that can be reproduced by intersecting a plane and a ouble-napped right cone. That's why they are commonly refered to as the conic section.
Conics includes parabolas, circles, ellipses, and hyperbolas. Among them, the parabola in the most common.
The conic section calculator, helps you get more information or some of the important parameters from a conic section equation.
How to identify a conic section by its equation
This conic equation identifier helps you identify conics by their equations eg circle, parabolla, elipse and hyperbola. The calculator also gives your a tone of other important properties eg radius, diretix, focal length, focus, vertex, major axis, minor axis etc
Another method of identifying a conic is through grapghing. This calculator also plots an accurate grapgh of the conic equation
Writing a standard form equation can also help you identify a conic by its equation. The calculator generates standard form equations
General (standard form) Equation of a conic section
Ax^2+Bxy+Cy^2+Dx+Ey+F=0,where A,B,C,D,E,F are constants
From the standard equation, it is easy to determine the conic type eg
B2−4AC<0 , if a conic exists, then it is a circle or ellipse
B2−4AC=0, if a conic exists, then it is a parabola
B2−4AC>0 , if a conic exists, it is a hyperbola
More About Circles
Geometrically, a circle is defined as a set of points in a plane that are equidistant from a certain point, this distance is commonly refered to as the radius.
Circle Equations Examples:
Center (0,0): x^2+y^2=r^2Center (h,k):(x−h)2+(y−k)2=r2.
where r is the radius
Given any equation of a circle, you can find the center, and radius by completing square method. Our calculator, helps you find the center and the radius of a circle for any equation.
graph of a Circle: Center: (0,0), Radius: 5
Parabolas
In technical terms, a parabolla is a seto of points that are equidistant from a line (refered to as the directrix) and a point on the line called the focus.
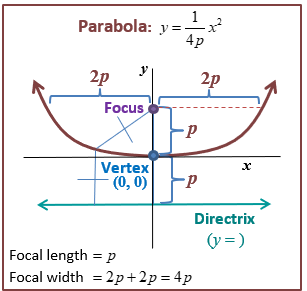
Parabolas are commonly occuring conic section. A parabola can be represented in the form
y=a(x−h)2+k, where (h,k) is the vertex and x=h is the axis of symmetry or line of symmetry; Note: this is the representation of an upward facing parabola.
The above can also be represented as
this is a vertical parabola. Note that this can also be written y−k=a(x−h)2 or b(y−k)=(x−h)2+k, where b=1a. The line of symmetry
For a horizontal parabola (line of axis is parallel to the x -axis)
x=a(y−k)2+h, where (h,k) is the vertex, and y=k is the line of symmetry
Ellipses
Techinically, an elipse is defined as a set of points whose distance from two fixed points (called the foci) inside the ellipse is always the same, d1+d2=2a.
The general equation of an elipse:
(x−h)^2/a^2+(y−k)^2/b^2=1 where (h,k) is the center
Define c^2=a^2−b^2
The eccentricity of an ellipse c/a, is a measure of how close to a circle the ellipse
Example Ploblem:
Find the vertices, co-vertices, foci, and domain and range for the following ellipses; then graph: (a) 6x^2+49y^2=441 (b) (x+3)^2/4+(y−2)^2/36=1
Solution: Use the Calculator to Find the Solution of this and other related problems.
The Hyperbolas
Generally, a hyperbola looks like two oposite facing parabollas, that are symmetrical.
Geometrically, a hyperbola is defined as a set of points whose distances from two fixed points (the foci) inside the hyperbola is always the same, d1−d2=2a.
Where '2a' is known as the focal radius or ocal radii distance, focal constant, or constant difference.
The general equation of a hyperbola:
(x−h)^2/a^2-(y−k)^2/b^2=1 where (h,k) is the center
